Spatial Modelling with SPDEs

Data preprocessing

In the following, we are going to work with the meuse dataset. This dataset contains measurements of zinc concentrations in the soil near the Meuse river.

We begin by downloading the dataset.

meuse_path = joinpath(@__DIR__, "meuse.csv")
meuse_URL = "https://gist.githubusercontent.com/essicolo/91a2666f7c5972a91bca763daecdc5ff/raw/056bda04114d55b793469b2ab0097ec01a6d66c6/meuse.csv"
download(meuse_URL, meuse_path)

"/home/runner/work/GaussianMarkovRandomFields.jl/GaussianMarkovRandomFields.jl/docs/build/tutorials/meuse.csv"

We load the CSV file into a DataFrame and inspect the first few rows.

using CSV, DataFrames
df = DataFrame(CSV.File(meuse_path))
df[1:5, [:x, :y, :zinc]]

5×3 DataFrame

Row	x	y	zinc
	Int64	Int64	Int64
1	181072	333611	1022
2	181025	333558	1141
3	181165	333537	640
4	181298	333484	257
5	181307	333330	269

Let us visualize the data. We plot the zinc concentrations as a function of the x and y coordinates.

using Plots
x = convert(Vector{Float64}, df[:, :x])
y = convert(Vector{Float64}, df[:, :y])
zinc = df[:, :zinc]
scatter(x, y, zcolor = zinc)

Finally, in classic machine learning fashion, we split the data into a training and a test set. We use about 85% of the data for training and the remaining 15% for testing.

using Random
train_idcs = randsubseq(1:size(df, 1), 0.85)
test_idcs = [i for i in 1:size(df, 1) if isempty(searchsorted(train_idcs, i))]
X = [x y]
X_train = X[train_idcs, :]
X_test = X[test_idcs, :]
y_train = zinc[train_idcs]
y_test = zinc[test_idcs]
size(X_train, 1), size(X_test, 1)

(131, 24)

Spatial Modelling

Matern Gaussian processes (GPs) are a powerful model class commonly used in geostatistics for such data. Unfortunately, without using any further tricks, GPs have a cubic runtime complexity. As the size of the dataset grows, this quickly becomes prohibitively expensive. In the tutorial on Autoregressive models, we learned that GMRFs enable highly efficient Gaussian inference through sparse precision matrices. Can we combine the modelling power of GPs with the efficiency of GMRFs?

Yes, we can: [1] told us how. It turns out that Matern processes may equivalently be interpreted as solutions of certain stochastic partial differential equations (SPDEs). If we discretize this SPDE appropriately – for example using the finite element method (FEM) – we get a discrete GMRF approximation of a Matern process. The approximation quality improves as the resolution of the FEM mesh increases. If this all sounds overly complicated to you, fear not! GaussianMarkovRandomFields.jl takes care of the technical details for you, so you can focus on the modelling.

We create a Matern latent model directly from the spatial coordinates. Internally, GaussianMarkovRandomFields.jl computes a convex hull around the scattered data, generates a FEM mesh, and sets up the SPDE discretization automatically.

Once we have the latent model, we need to instantiate it for a concrete range parameter. This architecture makes it easy to construct the same GMRF structure many times for different hyperparameter values.

using GaussianMarkovRandomFields
latent_model = MaternModel(X; smoothness = 1)
u_matern = latent_model(range = 400.0)

GMRF{Float64} with 698 variables
  Algorithm: LinearSolve.DefaultLinearSolver
  Mean: [0.0, 0.0, 0.0, ..., 0.0, 0.0, 0.0]
  Q_sqrt: not available

Next, we create an observation model for function value observations at the training points. PointEvaluationObsModel expresses that we're observing the value of our latent field at some specified points. Normal could've been replaced e.g. by Poisson to observe counts at the evaluation points instead – GLM style. As before, we need to pass hyperparameters to get a concrete object (an ObservationLikelihood). Once we have a concrete GMRF and a concrete observation likelihood, we can form a posterior through gaussian_approximation.

import Distributions
obs_noise_std = 0.32
obs_model = PointEvaluationObsModel(latent_model.discretization, X_train, Distributions.Normal)
obs_lik = obs_model(y_train; σ = obs_noise_std)
u_cond = gaussian_approximation(u_matern, obs_lik)

GMRF{Float64} with 698 variables
  Algorithm: LinearSolve.DefaultLinearSolver
  Mean: [72.24830414266613, 126.16814794857689, 59.14353433815095, ..., 23.859493707411747, 247.69561108831164, 242.96830721790695]
  Q_sqrt: not available

Next, we can evaluate the RMSE of the posterior mean on the test data. conditional_distribution gives us the predictive distribution p(y | x) for fixed x.

obs_model_test = PointEvaluationObsModel(latent_model.discretization, X_test, Distributions.Normal)
pred_dist_train = conditional_distribution(obs_model, mean(u_cond); σ = obs_noise_std)
pred_dist_test = conditional_distribution(obs_model_test, mean(u_cond); σ = obs_noise_std)
rmse = (a, b) -> sqrt(mean((a .- b) .^ 2))
rmse(mean(pred_dist_train), y_train), rmse(mean(pred_dist_test), y_test)

(57.51277796423521, 283.94940140642285)

We can also visualize the posterior mean and standard deviation. To this end, we write the corresponding vectors to a VTK file together with the grid data, which can then be visualized in e.g. Paraview.

using Ferrite
VTKGridFile("meuse_mean", latent_model.discretization.dof_handler) do vtk
    write_solution(vtk, latent_model.discretization.dof_handler, mean(u_cond))
end
using Distributions
VTKGridFile("meuse_std", latent_model.discretization.dof_handler) do vtk
    write_solution(vtk, latent_model.discretization.dof_handler, std(u_cond))
end

VTKGridFile for the closed file "meuse_std.vtu".

In the end, our posterior mean looks like this: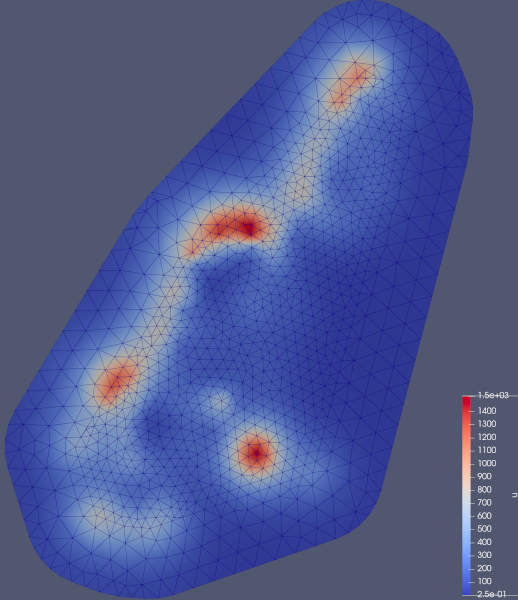

And the posterior standard deviation looks like this: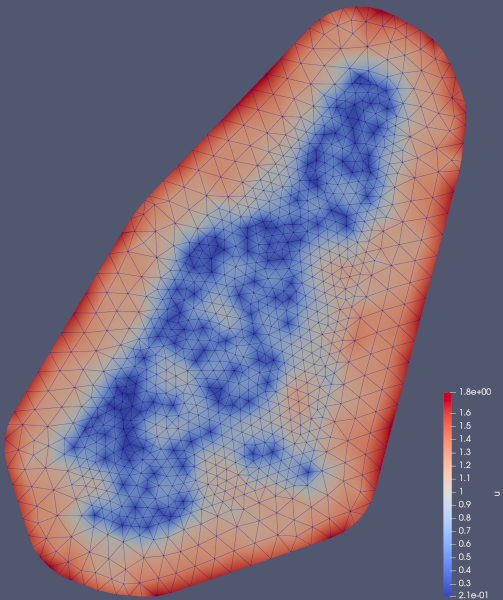

Final note

We have seen how to combine the modelling power of GPs with the efficiency of GMRFs. This is a powerful combination that allows us to model spatial data efficiently and accurately. Note that these models are still sensitive to the choice of hyperparameters, i.e. the range and smoothness of the Matern process. So it's quite likely that you may find better hyperparameters than the ones used in this tutorial.

---

This page was generated using Literate.jl.